В прошлом году я нашёл на Youtube одного замечательного человека, популяризатора математики (или евангелиста как сейчас говорят). Алексей Савватеев проводит лекции для всех желающих, и рассказывает о математике просто, в частности и о теории игр. До этого я слышал о теории игр отрывочно, и не понимал что это, да и вообще с высшей математикой у меня не особо ладилось в универе. В общем если кратко то теория игр — это способ выбора оптимального хода в игровой ситуации, когда каждый игрок предполагает что сделают другие игроки и на основе этого меняет свою стратегию, и так итерациями до тех по пока не наступит равновесие, но лучше посмотрите Алексея Савватеева он здорово объясняет. От него я узнал много интересного, и даже немного перестал боятся математики, например такая штука как парадокс Браеса — когда появление дополнительной дороги между пунктами А и Б увеличивает пробки!
Также он рассказывал о задаче о трёх вдовах. В Талмуде описана такая ситуация: некий мужчина имеет трёх жён (в те далёкие времени многожёнство было разрешено у иудеев), с каждой из которых составляется брачный контракт, в котором в числе прочего указывается сколько зуз (тогдашняя денежная единица) полагается выделить вдове из наследства в случае смерти мужа. Но что делать если наследство меньше чем сумма претензий всех жён? Талмуд предлагает решать проблему так:

Даны три случая с разным размером наследства 100, 200 и 300 зуз. В первом случае предлагается между всеми делить поровну, в третьем пропорционально, а во втором неким, на первый взгляд, абсолютно нелогичным образом. По сути — это классическая задача о банкротстве, в современном мире в таких ситуациях поступают как в третьем варианте — делят пропорционально. Талмуд — это как сборник use cases, там описано много различных ситуаций, и как поступать в них, но само правило при этом может быть не описано, видимо древние мудрецы переоценили своих потомков. На протяжении последних столетий многих мучил вопрос: по какому принципу решается эта задача, какова общая формула? И только относительно недавно в 1985 г. профессор Роберт Ауман вместе с Томасом Шеллингом разгадали формулу, это оказался нуклеолус, описанный в 1969 г. другим израильским учёным. Нуклеолус — сложная концепция, прочитав википедию и пару статей я так ничего и не понял. Вопрос сугубо практический, а как считать? На входе имеем наследство и суммы на которые претендуют наследники, на выходе кому сколько достанется. И я начал гуглить тщательнее…
Самое ценное что мне удалось найти это статья https://www.researchgate.net/publication/265440203_How_the_Talmud_Divides_an_Estate_Among_Creditors с более детальным описанием этой задачи в талмуде и её решением и лекцию Роберта Аумана в Москве http://gaidarfund.ru/articles/1983/. Лекция очень сильная, невольно проникаешься уважением к такому сильному наследию древних мудрецов. А Ауман и Шеллинг, думая над этим и прикладывая к современному миру в итоге получили нобелевскую премию по экономике в 2005 году.
Стало ясно что в основе этого дележа лежит принцип равного деления только того что оспариваются участники. Простейший пример из Талмуда на эту тему известен каждому еврейскому школьнику: на площади два человека делят одежды, один утверждает что всё принадлежит ему, другой говорит что половина принадлежит ему, как поступить в этом случае? Следует разделить пополам только то что оспаривается, т.е. один получит 3/4 другой 1/4. Тем не менее, как считать задачу со вдовами до сих пор непонятно )
И тут на помощь пришли картинки из статьи, это гидравлическая аналогия которую придумал Марек Камински, слушая лекцию посвященную открытию Аумана-Шеллинга, вот что он пишет в своей публикации 2000-го г.: «Сидя в классе, я постоянно пытался вообразить параметрическое представление решения из Талмуда, и недовольный собой, я перестал слушать и задумался об альтернативе. Гидравлическая аналогия пришла ко мне в голову во время одной из таких необъяснимых вспышек». Почти как Менделеев.
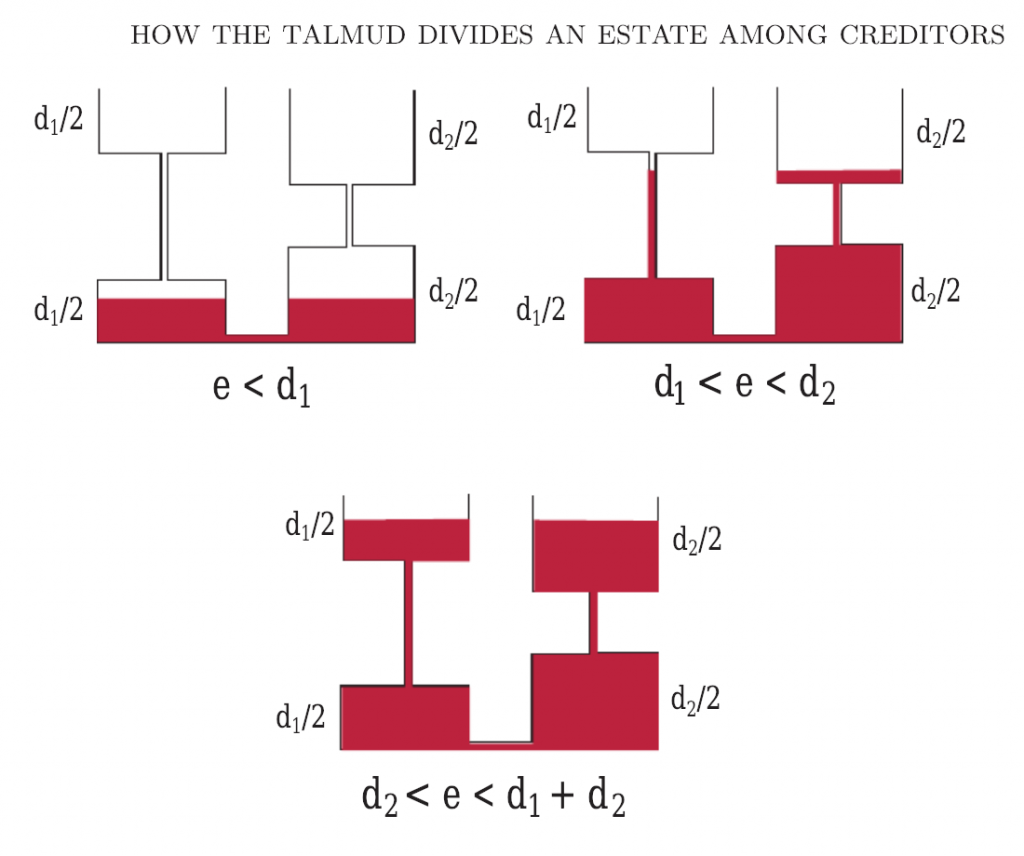
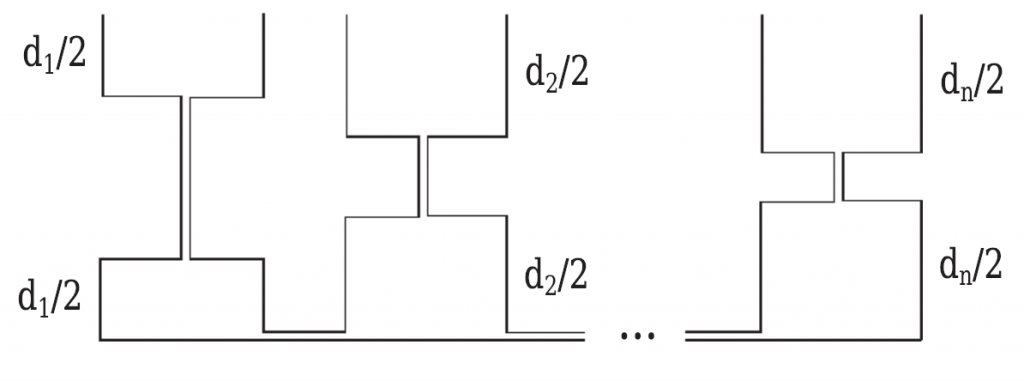
Высота каждый сосуда — это размер требований, каждый сосуд поделён на две части, объём жидкости — это размер наследства. Здесь результат можно получить аналитически, что я и сделал https://gist.github.com/holyketzer/a67c18d60752d700eefe2c073d273d4f. Решение не отличается особой элегантностью, но проще сделать я не смог, зато есть тесты.
Имея такую гидравлическую аналогию гораздо проще представить что пару тысяч лет назад, люди без современного мат. аппарата могли найти такое нетривиальное решение проблемы, и при этом считали его эталонным и само собой разумеющимся. Ну и кстати согласно Талмуду современные правила в области банкротства устроены несправедливо.
